RenzWK
00giovedì 3 maggio 2012 01:42
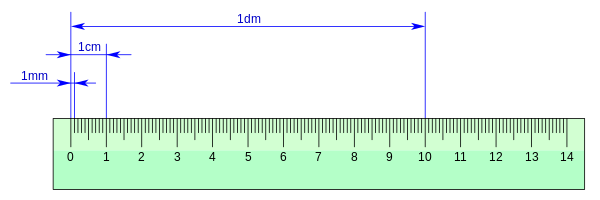
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Il centimetro (simbolo cm) è l'unità di misura di lunghezza fondamentale del sistema CGS, ma anche un'unità derivata del Sistema Internazionale.
Parliamone
![[SM=x2584176]](https://im0.freeforumzone.it/up/0/11/10151015.gif)
Mizar the game
00giovedì 3 maggio 2012 09:25
La successione di Fibonacci è una successione di numeri interi naturali definibile assegnando i valori dei due primi termini, F0:= 0 ed F1:= 1, e chiedendo che per ogni successivo sia Fn := Fn-1 + Fn-2 con n>1. In pratica si tratta di una successione di numeri in cui un numero è il risultato della somma dei due precedenti.
La sequenza prende il nome dal matematico pisano del XIII secolo Leonardo Fibonacci e i termini di questa successione sono chiamati numeri di Fibonacci. L'intento di Fibonacci era quello di trovare una legge che descrivesse la crescita di una popolazione di conigli. Assumendo che: la prima coppia diventi fertile al compimento del primo mese e dia alla luce una nuova coppia al compimento del secondo mese; le nuove coppie nate si comportino in modo analogo; le coppie fertili, dal secondo mese di vita, diano alla luce una coppia di figli al mese; avremo che se partiamo con una singola coppia dopo un mese una coppia di conigli sarà fertile, e dopo due mesi due coppie di cui una sola fertile, nel mese seguente avremo 2+1=3 coppie perché solo la coppia fertile ha partorito, di queste tre ora saranno due le coppie fertili quindi nel mese seguente ci saranno 3+2=5 coppie, in questo modo il numero di coppie di conigli di ogni mese descrive la successione dei numeri di Fibonacci.
I primi 42 numeri di Fibonacci (includendo lo 0) sono:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 (=F10)
89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 (=F20)
10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040 (=F30),
1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141 (=F41)
Nella OEIS di Neil Sloane la successione di Fibonacci ha la sigla A000045. I numeri di Fibonacci godono di una gamma stupefacente di proprietà, si incontrano nei modelli matematici di svariati fenomeni e sono utilizzabili per molti procedimenti computazionali; essi inoltre posseggono varie generalizzazioni interessanti. A questi argomenti viene espressamente dedicato un periodico scientifico, The Fibonacci Quarterly.
Indice [nascondi]
1 Proprietà
1.1 Relazioni con il triangolo di Tartaglia ed i coefficienti binomiali
1.2 Numeri di Fibonacci e fattori comuni
1.3 Numeri di Fibonacci vicini
1.4 Numeri di Fibonacci primi
1.5 Numeri di Fibonacci, teorema di Carmichael e fattori primi caratteristici
1.6 Proprietà di divisibilità
1.7 Primalità e compositezza
1.8 Teorema di Morrison
1.9 Pseudoprimi di Fibonacci
1.10 Relazioni con il massimo comun divisore e la divisibilità
2 Altre proprietà
3 Algoritmo di Euclide con ciclo più lungo
4 Frazioni continue
5 Generalizzazioni
5.1 Calcolo con la matrice M
5.2 Successioni Tribonacci e Tetranacci
6 Numeri complessi di Fibonacci
6.1 Proprietà dei numeri complessi di Fibonacci
7 Sequenza random di Fibonacci (sequenza di Vibonacci)
7.1 Costante di Viswanath
8 Sequenze Repfigit
8.1 Numeri Repfigit
8.2 Numeri Repfigit inversi
8.3 Congetture
9 Numeri Fibonacci e legami con altri settori
9.1 In chimica
9.2 Nella musica
9.3 In botanica
9.4 Nel corpo umano
9.5 In geometria e in natura
9.6 Nell'arte
9.7 Nell'economia
9.8 In informatica
9.9 Nei frattali
9.10 In elettrotecnica
10 Note
11 Bibliografia
12 Voci correlate
13 Bibliografia e riferimenti
14 Altri progetti
15 Collegamenti esterni
Proprietà [modifica]
Nelle formule che seguono talora scriveremo F(n) invece di Fn.
La successione di Fibonacci possiede moltissime proprietà di grande interesse. Certamente la proprietà principale, e maggiormente utile nelle varie scienze, è quella per cui il rapporto Fn / Fn-1, ossia tra un termine e il suo precedente, al tendere di n all'infinito tende al numero algebrico irrazionale chiamato sezione aurea o numero di Fidia. Quindi:
dove
Bisogna anche notare come, proseguendo via via per la sequenza, il rapporto risulti alternativamente maggiore e minore della costante limite.
Naturalmente il rapporto tra un numero di Fibonacci e il suo successivo tende al reciproco della sezione aurea .
Conviene anche ricordare:
a)
b)
in accordo con la definizione di sezione aurea come il numero positivo tale che , equazione che, quando vincolata alla condizione , ammette l'unica soluzione .
Si noti poi come l'opposto del reciproco del numero di Fidia che compare nella b) costituisca la seconda soluzione, a segno negativo, dell'equazione algebrica riportata nella definizione. Esso espone proprietà altrettanto interessanti di quelle del suo omologo positivo.
Cartello divulgativo sulle proprietà della successione di Fibonacci (Riserva naturale speciale del Bosco del Vaj)
Ragionamenti analoghi possono essere applicati per ottenere altri rapporti irrazionali costanti; per esempio dividendo ogni numero per il secondo successivo si ottiene 0,382 e dividendo ogni numero per il terzo successivo si ottiene 0,236, mentre dividendo ogni numero per il secondo precedente si ottiene 2,618 e dividendo ogni numero per il terzo precedente si ottiene 4,236.
Questi sei rapporti (0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236) sono inoltre molto utilizzati nella teoria delle onde di Elliott, argomento molto importante dell'analisi tecnica dei mercati finanziari.
Si trova anche che l'n-simo numero di Fibonacci si può esprimere con la formula:
.
Questa elegante formula prende il nome da Jacques Binet, che la ricavò nel 1843; tuttavia essa era già nota nel XVIII secolo ad Eulero, Abraham de Moivre e Daniel Bernoulli.
Talora risulta comodo servirsi della successione bilatera costituita da numeri interi Fn:= 0 definiti per n intero qualsiasi aggiungendo alle precedenti le definizioni
A partire dai numeri di Fibonacci e dalla sezione aurea si possono definire alcune funzioni speciali: coseno iperbolico di Fibonacci, cotangente iperbolica di Fibonacci, seno iperbolico di Fibonacci, tangente iperbolica di Fibonacci.
Relazioni con il triangolo di Tartaglia ed i coefficienti binomiali [modifica]
Le prime righe del Triangolo di Tartaglia sono le seguenti:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Se si considerano le diagonali che da sinistra salgono verso destra nel triangolo di Tartaglia, e se si sommano i numeri intercettati da tali diagonali, si individuano i numeri di Fibonacci. Per facilitarci il compito il triangolo lo riscriviamo nel seguente modo:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Partiamo dal "primo 1 prima riga" con una diagonale che va da sinistra verso destra in alto la cui somma è 1, poi "il secondo 1 seconda riga" altrettanto dà 1, "il terzo 1 terza riga" intercetta l'1 a destra della seconda riga e la somma è 2, il quarto 1 quarta riga con la sua diagonale che va da sinistra a destra verso l'alto intercetta un 2 e la somma è 3 etc.
La relazione esistente è:
Numeri di Fibonacci e fattori comuni [modifica]
Ogni numero di Fibonacci è un fattore di (un numero infinito di) numeri di Fibonacci successivi oppure ogni k-th numero di Fibonacci è un multiplo di F (k).
È equivalente a dire matematicamente che:
Se Fib(k) = m allora Fib(n*k) = t con m|t
Si dimostra in due modi possibili:
1.mo modo:
Dai coefficienti binomiali
2.do modo:
Costruiamo una tabella mettendo x se il risultato m di m=Fib(k) non è un divisore di Fib(k)
i 3 4 5 6 7 8 9 10 11 12
Fib(i) 2 3 5 8 13 21 34 55 89 144
2=Fib(3) * x x * x x * x x *
3=Fib(4) x * x x x * x x x *
5=Fib(5) x x * x x x x * x x
Proseguendo si vede ad esempio che:
2 è un fattore ogni 3 Fib(k)
3 è un fattore ogni 4 Fib(k)
5 è un fattore ogni 5 Fib(k)
etc
Numeri di Fibonacci vicini [modifica]
I numeri di Fibonacci vicini non hanno fattori in comune oppure Fib (k) e Fib (k +1) sono coprimi.
Se Fib(k)=m*a e Fib(k+1)=m*b (con fattore m in comune) per assurdo, allora
Fib(k+2)=Fib(k)+Fib(k+1)=m*(a+b)
Il che vorrebbe dire che tutta la successione di Fibonacci dovrebbe avere lo stesso fattore m in comune, il che non è vero.
Numeri di Fibonacci primi [modifica]
Come corollario di prima, se l'indice di un numero di Fibonacci è un multiplo di k, il numero di Fibonacci è composto.
Se il numero di Fibonacci è un primo lo è anche l'indice.
Non è vero il contrario. Infatti ad esempio
F (19) = 4.181 e F (19) non è primo perché 113x37 = 4.181
Il più grande numero primo di Fibonacci F (81.839) è stato segnalato in aprile 2001 da David Broadbent e Bouk de Water.
La serie di numeri indice dei numeri primi di Fibonacci è A001605 Sloane.
Numeri di Fibonacci, teorema di Carmichael e fattori primi caratteristici [modifica]
Se guardiamo i fattori primi di un numero di Fibonacci, ci sarà almeno uno di loro che non è mai apparso come un fattore in ogni numero di Fibonacci in precedenza.
Questo è noto come Teorema di Carmichael e si applica a tutti i numeri di Fibonacci, tranne nei seguenti casi particolari:
Fib (1) = 1 (non ha fattori primi)
Fib (2) = 1 (non ha fattori primi)
Fib (6) = 8, che ha solo il fattore primo 2, che è anche Fib (3)
Fib (12) = 144, che anche solo il 2 e 3, come i suoi fattori primi e questi sono apparsi in precedenza come Fib (3) = 2 e Fib (4) = 3
In tutti gli altri casi è vero il Teorema.
Quindi, se i = p è primo, allora p non avrà fattori; quindi Fib (p), inoltre non può avere prima numeri di Fibonacci come i suoi fattori.
Si noti che questo non significa Fib (p), deve essere il primo, solo che nessun numero di Fibonacci più piccoli può essere un fattore.
Abbiamo trovato un esempio di questo in Fib (19) che è 4.181 = 37 x 113
Qui anche se 19 è un numero primo, Fib (19) non lo è.
Il Teorema di Carmichael dice che non ci sono fattori primi di Fib (p) che si verificano in precedenza nell’ elenco dei numeri di Fibonacci.
Quindi, se p è un numero primo, allora sono possibili due casi:
Entrambi p e Fib (p) sono primi e nel qual caso questa è la prima volta che troviamo il numero primo p nella lista dei fattori di Fibonacci.
In alternativa se Fib (p) ha elementi, almeno uno di loro (in realtà tutti), è una novità o un elemento caratteristico.
Per dirla in modo più semplice per un numero primo p, Fib (p) è un primo oppure è un prodotto di fattori primi che sono caratteristici (appaiono per la prima volta nella nostra lista di fattori di Fibonacci).
Un fattore primitivo di Fib(n) è congruente a 1 (mod n), con l'eccezione n = 5.
Se n = 3 (mod 10) e n è un divisore primitivo di Fib(n + 1), allora n è primo. Se n = 1 (mod 10) e n è un divisore primitivo di Fib(n − 1), allora n è primo (citato per la prima volta da Édouard Lucas, ma non dimostrato).
Proprietà di divisibilità [modifica]
I numeri di Fibonacci godono in generale delle seguenti proprietà di divisibilità:
Se allora
dove il simbolo x | y significa che x è un divisore di y; mentre il simbolo è il simbolo di Legendre che vale 1 se rappresenta il quadrato modulo p, -1 nel caso contrario.
Ad esempio nel caso mod p = mod 7 =1 nei seguenti casi 1 = 1x1 mod 7, 4=2x2 mod 7; mentre 3 non è il quadrato di un numero modulo 7 per cui =-1
Un altro risultato è il seguente: Scelti n + 1 numeri di Fibonacci da un insieme: F1, F2, F3, ... , F2n: allora uno dei numeri scelti divide un altro, esattamente (Weinstein 1966).
Mihàly Bencze trovò una nuova proprietà di divisibilità con una nuova sequenza. La sequenza ha i primi quattro valori fissati e la regola B(n + 4) = B(n + 1) + B(n).
n 0 1 2 3 4 5 6 7 8 9 10 11 12 13
B(n) 4 0 0 3 4 0 3 7 4 3 10 11 7 13
Ora si osserva che B(n) è sempre divisibile per n, quando n è un numero primo (Bencze 1998).
Primalità e compositezza [modifica]
Se p è un numero primo maggiore di 7 e p = 2 (mod 5) oppure p = 4 (mod 5) e 2p − 1 è un numero primo (una condizione che ricorda quella sulla primalità di Sophie Germain), allora (2p − 1) | Fp, quindi Fp è composto.
Se p è primo allora non è un quadrato perfetto ad eccezione di p=5, nel qual caso però è , con m non quadrato perfetto.
Teorema di Morrison [modifica]
Il Teorema di Morrison permette attraverso i numeri di Fibonacci di determinare la primalità di N.
Se N = R*F - 1 con F > e =-1 e per ogni q | F si ha che:
N | Fib(N+1)
MCD(N, Fib((N+1)/q))=1
allora N è primo.
Tale Teorema permette di lavorare con i numeri del tipo N=2^n-1 (numeri di Mersenne)
Pseudoprimi di Fibonacci [modifica]
Se N è composto e soddisfa le proprietà di divisibilità dei numeri di Fibonacci
N | Fib(N - )
N | Fib(N) -
allora N è uno pseudoprimo di Fibonacci
Relazioni con il massimo comun divisore e la divisibilità [modifica]
Un'importante proprietà dei numeri di Fibonacci riguarda il loro massimo comun divisore. Infatti è soddisfatta l'identità
(Teorema di Vorob’ev)
Da questo segue che F(n) è divisibile per F(m) se e solo se n è divisibile per m. Questa proprietà è importante perché ne segue che un numero di Fibonacci F(n) può essere un numero primo solamente se n stesso è un numero primo, con l'unica eccezione di F4=3 (l'unico numero di Fibonacci per cui potrebbe essere divisibile è F2=1).[1] Il viceversa tuttavia non è vero: F(19), ad esempio, è uguale a 4181=37*113.
Non è noto se i numeri primi che sono anche numeri di Fibonacci siano o meno infiniti.
Inoltre si può dimostrare che ogni numero primo divide almeno uno, e di conseguenza infiniti, numeri di Fibonacci.
Altre proprietà [modifica]
Tra le altre proprietà minori della sequenza di Fibonacci vi sono le seguenti.
Charles Raine trovò che se si considerano 4 numeri di Fibonacci di seguito e consideriamo un triangolo rettangolo con cateti a, b e ipotenusa c, allora è: a=, b=2*, . Se esaminiamo ad esempio la sequenza di Fibonacci e prendiamo solo ...3,5,8,13,... allora è a=3*13=39, b=2(5*8)=80, c=89. Sommando i quadrati otteniamo
Dati quattro numeri di Fibonacci consecutivi, il prodotto del primo col quarto è sempre pari al prodotto del secondo col terzo aumentato o diminuito di 1.
Se si prende la sequenza dei quadrati dei numeri di Fibonacci, e si costruisce una sequenza sommando a due a due i numeri della prima sequenza, la sequenza risultante è costituita da tutti e soli i numeri di Fibonacci di posto dispari;
Data la sequenza dei numeri di Fibonacci di posto dispari, se si costruisce la sequenza ottenuta sottraendo a due a due i numeri adiacenti della prima sequenza, si ottiene la sequenza dei numeri di Fibonacci di posto pari.
Ogni numero di Fibonacci corrisponde alla somma dei numeri che lo precedono eccetto l'ultimo, aumentata di 1.
Gli unici numeri di Fibonacci che sono anche quadrati sono 0, 1 e 144, come dimostrato nel 1963 da John H. E. Cohn[2].
L'identità di Cassini, scoperta nel 1680 da Jean-Dominique Cassini, afferma che per ogni intero n,
Tale identità è stata generalizzata nel 1879 da Eugène Charles Catalan:
La somma dei reciproci dei numeri di Fibonacci converge, come si può vedere applicando il criterio del rapporto, ricordando che il rapporto tra due numeri di Fibonacci consecutivi tende a . La somma di questa serie è circa 3,35988566624; è stato dimostrato che questo numero è irrazionale. Si può ricavare già da 100 termini con PARI/GP: sum(i=1,100,1.0/fibonacci(i))
Algoritmo di Euclide con ciclo più lungo [modifica]
Lamé dimostrò nel 1844 che l'algoritmo di Euclide ha un ciclo più lungo se in input ci sono numeri di Fibonacci
Frazioni continue [modifica]
Ci sono legami con le frazioni continue da parte dei numeri di Fibonacci, ma anche con le frazioni di Farey e la sezione aurea.
Una particolare frazione continua infinita è la sezione aurea = (0,1,1,1,1,1,1,1,1,…)
La frazione continua precedente si può anche considerare come vari pezzetti di termini convergenti; ad esempio:
(0) = 0
(0, 1) = 1
(0, 1, 1) = 1/2
(0, 1, 1, 1) = 2/3
(0, 1, 1, 1, 1) = 3/5
(0, 1, 1, 1, 1, 1) = 5/8
(0, 1, 1, 1, 1, 1, 1) = 8/13
I vari pezzetti visti prima ci danno due legami inattesi della sezione Aurea: uno con la successione di Fibonacci, l’altro con la successione di Farey.
Difatti notiamo tra i pezzetti il ripetersi della sequenza 1, 2, 3, 5, 8, 13, … come nei numeri di Fibonacci. Escludendo (0), per ottenere il terzo elemento si devono sommare i primi due, per ottenere poi il successivo termine si devono sommare i precedenti due etc.
Sempre dai pezzetti si osserva che due successivi convergenti della sezione aurea soddisfano la relazione (ps - qr) = 1. Ad esempio con 5/8 e 8/13 si ha che 5*13-8*8=65-64=1, come nella serie di Farey.
Generalizzazioni [modifica]
Una generalizzazione si può ottenere ponendo:
W0(a, b, h, k) = a, W1(a, b, h, k) = b e per ogni n > 1 sia Wn(a, b, h, k) = hWn-1(a, b, h, k) – kWn-2(a, b, h, k)
Le sono successioni ricorrenti lineari, dove ogni elemento è combinazione lineare dei due precedenti.
Diciamo successione generalizzata di Fibonacci la sequenza Wn (a, b, h, k) con valori iniziali 0 e 1:
La classica successione di Fibonacci è: {} = {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... }
Diciamo successione generalizzata di Lucas la sequenza:
La classica successione dei numeri di Lucas è: {} = {2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199 • • • }
I numeri di Lucas e quelli di Fibonacci sono collegati da moltissime relazioni. Si noti per esempio che: 1+2=3, 1+3=4, 2+5=7, 3+8=11, …. , Fib(k) + Fib(k+2) = L(k+1)
Quindi da quanto visto sopra una successione di Fibonacci può anche non cominciare necessariamente con due 1. Questa successione è detta successione di Fibonacci generica o generalizzata. Ogni successione generica di Fibonacci rispetta però una singolare caratteristica, la somma dei primi 10 elementi sarà sempre uguale a 11 volte il settimo elemento. La dimostrazione è molto semplice: elenchiamo i primi 10 elementi in questo modo:
1º elemento: m
2º elemento: n
3º elemento: m + n
4º elemento: m + 2n
5º elemento: 2m + 3n
6º elemento: 3m + 5n
7º elemento: 5m + 8n
8º elemento: 8m + 13n
9º elemento: 13m + 21n
10º elemento: 21m + 34n
Sommando tutti i dieci elementi, si otterrà 55m + 88n che è proprio uguale a 11 volte il settimo elemento.
Ogni successione generalizzata conserva la proprietà che il rapporto tra due numeri consecutivi tende alla sezione aurea. Una particolare successione di Fibonacci generalizzata, quella ottenuta ponendo m=2 e n=1, è detta successione di Lucas, dal matematico francese Édouard Lucas.
Calcolo con la matrice M [modifica]
Un metodo efficace per calcolare numeri di Fibonacci generalizzati con indice grande è fare ricorso alle matrici.
M =
=
Se
allora
I + M
dove
Successioni Tribonacci e Tetranacci [modifica]
La successione di Fibonacci può essere anche generalizzata non richiedendo che ogni numero sia la somma dei due precedenti, ma degli ultimi n, dove n è un qualsiasi numero intero. Se n=1 si ottiene una successione degenere i cui termini sono tutti 1, se n=2 si ottiene la successione di Fibonacci, mentre per n=3 e 4 si ottengono rispettivamente le cosiddette successione Tribonacci e Tetranacci. Caratteristica comune di queste successioni è che il rapporto tra due termini consecutivi tende alla radice reale compresa tra 1 e 2 del polinomio
Anche la somma dei reciproci degli elementi di questa successione converge (se n>1), come si può vedere facilmente considerando che ogni k-esimo elemento di una successione è maggiore o uguale del corrispondente elemento F(k) della successione di Fibonacci, e quindi il reciproco è minore.
Numeri complessi di Fibonacci [modifica]
Un numero complesso di Fibonacci è un numero complesso la cui parte reale è un numero di Fibonacci.
Ad esempio z=8-i è un numero complesso di Fibonacci perché Re(z)=8=F(6).
Proprietà dei numeri complessi di Fibonacci [modifica]
Il rapporto di numeri complessi di Fibonacci con k dispari e n > 0 è tale che:
[F(k) - n*i] / [F(k-1)-(n-1)*i] = [F(k+n)+i*(-1)^(n-1)] / [F(k+(n-1)]
dove F(k+n)=
Ad esempio:
(5 - i ) / (3 - i) = (8 + i) / 5
(13 - i ) / (8 - i) = (21 + i) / 13
(8 - 2i) / (5 - i) = (21 - i) / 13
(13 - 3i)/(8 - 2i) = (55 + i)/34
Per k pari e n > 0 la formula non vale per i numeri complessi ma solo per i numeri interi sostituendo 1 a i, ovvero
[F(k) - n] / [F(k-1)-(n-1)] = [F(k+n)+(-1)^(n-1)] / [F(k+(n-1)]
dove F(k+n)=
Ad esempio:
(8 - 1) / (5 - 1) = (13 + 1) / 8
(13 - 2) / (8 - 1) = (34 - 1) / 21
(8 - 3)/(5 - 2) = (34 + 1) / 21
(8 - 3) / (5 - 2) = (34 + 1) / 21
Sequenza random di Fibonacci (sequenza di Vibonacci) [modifica]
Nel 1999, Divikar Viswanath, professore alla Michigan State University, ideò una sequenza random di Fibonacci. Tale sequenza fu detta sequenza di Vibonacci oppure sequenza random di Viswanath.
Viswanath creò tale sequenza in un esperimento statistico. Se si uguagliano i valori di addizione e sottrazione di testa e croce di una moneta, si ottiene una ugual probabilità di 1/2.
La successione matematicamente è definita come Vn = Vn-2 ± Vn-1 for n=3, 4, 5…[Hay].
In Mathematica la successione di Vibonacci è programmata come segue:
v[k_, 1] := v[k, 1] = 1
v[k_, 2] := v[k, 2] = 1
v[k_, n_] := v[k, n] = v[k, n-2] + (-1)^ Random[Integer,{0, 1}] v[k, n-1]
Costante di Viswanath [modifica]
Viswanath scoprì una costante simile al rapporto aureo nella sua successione. Dal momento che la sequenza non è sempre in crescita, Viswanath sapeva che la costante sarebbe stata inferiore al rapporto aureo. Tale costante fu da lui chiamata C, ma più tardi fu chiamata costante di Viswanath dai matematici Mark Embree e Lloyd M. Trefethen [Hay].
La costante coinvolge concetti come l'albero di Stern-Brocot e la Formula di Furstenberg.
Sequenze Repfigit [modifica]
Numeri Repfigit [modifica]
Il nome deriva da "replicating Fibonacci digit" ed indica i "numeri riproduttori di Fibonacci".
Si definisce numero Repfigit o numero di Keith un numero n intero, costituito da m digit d1d2...dm, che si rigenera all'interno di una sequenza del tipo
d1, d2, ..., dm, s1 = d1+d2+d3+...+dm, s2 = s1+d2+...+dm, s3 = s2+s1+d3+...+dm, ...
Generalizzando si consideri la sequenza definita da
sk = dk (k = 1, 2, …, m) sk = sum(i=1,m,sk-i) (k>m).
Se sk=n per qualche k, n è un numero riproduttore di Fibonacci o numero di Keith.
Esempi di repfigit
n=47 m=2 digit
4, 7, 11, 18, 29, 47
n=1535 m=4 digit
1, 5, 3, 7, 16, 31, 57, 111, 215, 414, 797, 1537
È nel 1987, che Michael Keith ha introdotto il concetto dei numeri riproduttori di Fibonacci.
Nel 1987 il numero repfigit più grande conosciuto era un numero di 7 cifre, 7.913.837. Nel novembre 1989, fu scoperto 44.121.607 e nello stesso anno il dottor Googol trovò che i numeri 129.572.008 e 251.133.297 sono repfigit nell'intervallo definito tra 100 e 1.000 milioni. Oggi sono stati scoperti numeri di questo tipo molto più grandi.
Numeri riproduttori di Fibonacci fino a 5 cifre
m=2 14 19 28 47 61 75
m=3 197 742
m=4 1104 1537 2208 2580 3684 4788 7385 7647 7909
m=5 31331 34285 34348 55604 62662 86935 93993
Vedi [1] A007629 in Sloane's OEIS per una lista completa.
Numeri Repfigit inversi [modifica]
Esistono anche i numeri di Keith inversi, detti sinteticamente revRepfigit.
Ad esempio 12 è un numero revRepfigit perché con la tecnica vista prima si può ottenere una sequenza che mi dà il numero rovesciato ovvero 21: 1,2,3,5,8,13,21
Sono revRepfigit anche 12, 24, 36, 48, 52, 71, 341, 682, 1285, 5532, 8166, 17593, 28421, 74733, 90711, 759664, 901921, 1593583, 4808691 etc.
Congetture [modifica]
Ci sono almeno due congetture da verificare:
1. Se i numeri repfigit sono infiniti.
2. Se esistono repfigit con m>34.
Numeri Fibonacci e legami con altri settori [modifica]
In matematica i numeri di Fibonacci sono legati in qualche modo alla sezione aurea, alla sequenza di Farey, alle frazioni continue, alla zeta di Fibonacci, alla zeta di Riemann, ai gruppi di Lie, ai frattali.
In Fisica sussiste il legame con la teoria delle stringhe. Molti altri legami sono evidenti con la biologia, la cristallografia, la musica, l'economia, l'arte, l'elettrotecnica, l'informatica, ecc. Tuttavia non mancano esempi di "avvistamenti" della serie di Fibonacci un po' forzati: lo rivelano Gael Mariani e Martin Scott dell'Università di Warwick, con un articolo su New Scientist del settembre 2005.
In chimica [modifica]
Recentemente in Germania scienziati internazionali hanno scoperto la comparsa del numero aureo 1,618 insieme al gruppo di simmetria E8 in un composto chimico (niobato di cobalto), portato artificialmente in uno stato quantistico critico (l'equivalente quantistico dei frattali).
Tramite il principio geometrico delle teorie di stringa si può trovare che i numeri di Fibonacci conservano la simmetria e sono abbastanza vicinissimi ai "Numeri di Lie", sui quali, invece, si basano i cinque gruppi eccezionali di simmetria G2, F4, E6, E7, E8.
E8 è proprio il gruppo coinvolto in tale recente ed importante scoperta. E8 ha dimensione 57, che è un numero di Lie per n = 7, infatti 7^2+7+1=57, vicinissimo al numero di Fibonacci 55=7^2+7-1 (i numeri di Lie e i numeri di Fibonacci hanno quindi lo stesso DNA geometrico (simmetria) e numerico corrispondente (parabola n^2+n+1 per i numeri di Lie, n^2+n+/-c con n primo e c molto piccolo). Ma il numero 248, collegato a E8, è anche 248 = 15^2+15+8=225+15+8 con numero vicino di Fibonacci 233=15^2+15-7
Nella musica [modifica]
La musica ha numerosi legami con la matematica, e molti ritengono che importante in essa sia il ruolo della sezione aurea e dei numeri di Fibonacci. Sul piano compositivo la sezione aurea attraverso la serie di Fibonacci può, ovviamente, essere rapportata a qualsiasi unità di misura concernente la musica, cioè durata temporale di un brano, numero di note o di battute, etc non sono comunque rari anche in questo caso facili entusiasmi dovuti a fraintendimenti numerici. Per esempio Paul Larson nel 1978 riscontrò nei Kyrie contenuti nel Liber Usualis il rapporto aureo a livello delle proporzioni melodiche, ma in mancanza di una documentazione che ne attesta la volontà di inserimento, la non casualità della cosa rimane tutta a livello puramente congetturale; medesime illazioni sono sempre state fatte che per le opere di Mozart, anche se recentemente John Putz, matematico all'Alma College, subitamente convinto anche lui tale teoria specialmente per quanto riguarda le sue sonate per pianoforte, dovette ricredersi riscontrando un risultato decente soltanto per la Sonata n. 1 in Do maggiore.
I musicologi hanno trovato altre applicazioni nei rapporti fra le durate (in misure) delle varie parti dei brani musicali, in particolare si trovano tali rapporti nelle opere di Claude Debussy[3][4]e di Béla Bartók[5][6]. Tra i compositori del XX secolo ricordiamo Stravinsky, Xenakis, Stockhausen (vedi il brano Klavierstück IX, dove si hanno frequenti rimandi alle successioni fibonacciane nelle segnature di tempo), Nono, Ligeti, Manzoni e Gubajdulina che disse a proposito di Bartok:
« [...] L'aspetto ritmico della musica di Bartók mi interessa moltissimo, al punto che vorrei studiare a fondo la sua applicazione della Sezione Aurea. »
Tuttavia è molto difficile stabilire se l'artista ha voluto consciamente strutturare l'opera con la sezione aurea o se piuttosto essa sia frutto della sua sensibilità artistica[7], dato che la sezione aurea si riscontra spesso in natura[8], come ad esempio nelle stelle marine, in ammoniti, conchiglie, ananas, pigne e nella forma di un uovo[9]. Infatti mentre alcuni ritengono che i sopra citati Debussy e Bartok impieghino deliberatamente la sezione aurea, per altri questo è meno scontato. D'altronde Debussy scrive al suo editore Durand (agosto 1903) esplicitamente:
(FR)
« Vous verrez, à la page 8 de "Jardins sous la Pluie", qu'il manque une mesure; c'est d'ailleurs un oubli de ma part, car elle n'est pas dans le manuscrit. Pourtant, elle est nécessaire, quant au nombre; le divine nombre [...]. »
(IT)
« Lei vedrà, alla pagina 8 di "Jardins sous la Pluie" che manca una misura; è inoltre una mancanza della mia parte, perché non è nel manoscritto. Ancora, è necessaria, per il numero; il numero divino [...]. »
Nel Novecento le avanguardie della musica colta e molti tra gli eredi del serialismo, come i già citati Karlheinz Stockhausen, György Ligeti e Iannis Xenakis, invece applicarono sistematicamente e intenzionalmente - differentemente dalla maggioranza dei loro predecessori - i numeri di Fibonacci alla musica, approfondendone lo studio e la conoscenza e facendo evolvere i precedenti utilizzi della matematica in musica, hanno introdotto un utilizzo più strutturato della matematica (soprattutto il calcolo delle probabilità e del computer per la composizione musicale). Xenakis in particolare ha fondato a tale fine, a Parigi nel 1972, un gruppo di ricerca universitario chiamato CEMAMU, che ha appunto come obiettivo l’applicazione delle conoscenze scientifiche moderne e del computer alla composizione musicale e alla creazione di nuovi suoni tramite sintetizzatori.
Anche la musica Rock, specialmente nel cosiddetto rock progressivo, si è confrontata con gli aspetti mistico-esoterici della sezione aurea, e più precisamente dalla serie di Fibonacci. L’esempio più emblematico è la musica dei Genesis, che hanno usato assiduamente la serie fibonacciana nella costruzione armonico-temporale dei loro brani: Firth of Fifth è tutto basato su numeri aurei: ad esempio ci sono assoli di 55, 34, 13 battute, di questi alcuni sono formati da 144 note, etc. Oltre ai Genesis, altre rock band hanno usato, seppure più sporadicamente, i numeri aurei nelle loro composizioni. Fra questi i Deep Purple nel brano Child in Time e i Dream Theater nell'album Octavarium, interamente concepito secondo il rapporto tra i numeri 8 e 5 e termini consecutivi della sequenza di Fibonacci. Risale invece al 2001 Lateralus album della band americana Tool che contiene il singolo omonimo "Lateralus" costruito fedelmente sulla serie di Fibonacci: i Tool fanno un sapiente uso dei primi elementi della successione di Fibonacci: contando infatti le sillabe della prima strofa si ottiene 1,1,2,3,5,8,5,3,2,1,1,2,3,5,8,13,8,5,3. Da notare che la canzone fa un continuo riferimento alla figura della spirale ([...] To swing on the spiral [...] Spiral out. Keep going [...]).
In botanica [modifica]
Quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro o cinquantacinque o ottantanove petali: i gigli ne hanno tre, i ranuncoli cinque, il delphinium spesso ne ha otto, la calendula tredici, l'astro ventuno, e le margherite di solito ne hanno trentaquattro o cinquantacinque o ottantanove.
I numeri di Fibonacci sono anche in altri fiori come il girasole; difatti le piccole infiorescenze al centro di girasole sono disposte lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario.
I pistilli sulle corolle dei fiori spesso sono messi secondo uno schema preciso formato da spirali il cui numero corrisponde ad uno della serie di Fibonacci. Di solito le spirali orientate in senso orario sono trentaquattro mentre quelle orientate in senso antiorario cinquantacinque (due numeri di Fibonacci); altre volte sono rispettivamente cinquantacinque e ottantanove, o ottantanove e centoquarantaquattro. Si tratta sempre di numeri di Fibonacci consecutivi.
Le foglie sono disposte sui rami in modo tale da non coprirsi l’una con l’altra per permettere a ciascuna di esse di ricevere la luce del sole. Se prendiamo come punto di partenza la prima foglia di un ramo e si contano quante foglie ci sono fino a quella perfettamente allineata spesso viene un numero di Fibonacci e anche il numero di giri in senso orario o antiorario che si compiono per raggiungere tale foglia allineata dovrebbe essere un numero di Fibonacci. Il rapporto tra il numero di foglie e il numero di giri si chiama “rapporto fillotattico” (vedi Fillotassi).
Nel corpo umano [modifica]
Il rapporto fra le lunghezze delle falangi del dito medio e anulare di un uomo adulto è aureo, come anche il rapporto tra la lunghezza del braccio e l'avambraccio, e tra la lunghezza della gamba e la sua parte inferiore.
In geometria e in natura [modifica]
La spirale di Fibonacci, creata mediante l'unione di quadrati con i lati equivalenti ai numeri della successione di Fibonacci.
Se si disegna un rettangolo con i lati in rapporto aureo fra di loro, lo si può dividere in un quadrato e un altro rettangolo, simile a quello grande nel senso che anche i suoi lati stanno fra loro nel rapporto aureo. A questo punto il rettangolo minore può essere diviso in un quadrato e un rettangolo che ha pure i lati in rapporto aureo, e così via.
La curva che passa per vertici consecutivi di questa successione di rettangoli è una spirale che troviamo spesso nelle conchiglie e nella disposizione dei semi del girasole sopra descritta e delle foglie su un ramo.
Nell'arte [modifica]
I numeri di Fibonacci sono stati usati in alcune opere d'arte; ad esempio Mario Merz li ha usati nell'installazione luminosa denominata Il volo dei numeri su una delle fiancate della Mole Antonelliana di Torino. Sulle mura di San Casciano in Val di Pesa, accanto ad un cervo imbalsamato, sono permanentemente installati i numeri al neon riportanti le cifre 55, 89, 144, 233, 377 e 610. Si tratta di una creazione di Merz realizzata in occasione della mostra Tuscia Electa del 1997. [2] Merz ha inoltre realizzato nel 1994 un'installazione permanente sulla ciminiera della compagnia elettrica Turku Energia a Turku, in Finlandia.
Inoltre il pittore austriaco Helmutt Bruck ha dipindo meravigliosi quadri omaggiando Fibonacci e producendo opere in serie di 21.
Anche a Barcellona e a Napoli è stata creata un'installazione luminosa: nella città spagnola si trova nell'area della Barceloneta, all'interno dell'area pedonale, dove i numeri sono posti a distanze proporzionali alla loro differenza, mentre a Napoli sono disposti a spirale all'interno della stazione "Vanvitelli" della Linea 1 della Metropolitana, e più precisamente sul soffitto che sovrasta le scale mobili quando, superate le obliteratrici, si scende all'interno della stazione vera e propria.
Nell'economia [modifica]
I numeri di Fibonacci sono utilizzati anche in economia nell'Analisi tecnica per le previsioni dell'andamento dei titoli in borsa, secondo la teoria delle onde di Elliott.
Studiando i grafici storici dei titoli, Ralph Nelson Elliott sviluppò un metodo basato su tredici conformazioni grafiche dette onde, simili per forma ma non necessariamente per dimensione.
A differenza di altre applicazioni grafiche come medie mobili, trendline, macd, rsi ecc. che si limitano ad indicare il livello di resistenza e di supporto e le angolature del trend "Il principio delle onde di Elliott" è l'unico metodo in grado di individuare un movimento del mercato dall'inizio alla fine e quindi di presumere i futuri andamenti dei prezzi.
In informatica [modifica]
I numeri di Fibonacci sono utilizzati anche nel sistema informatico di molti computer. In particolare vi è un complesso meccanismo basato su tali numeri, detto "Fibonacci heap" che viene utilizzato nel processore Pentium della Intel per la risoluzione di particolari algoritmi.
Nei frattali [modifica]
Nei frattali di Mandelbrot, governati dalla proprietà dell'autosomiglianza, si ritrovano i numeri di Fibonacci. L'autosomiglianza difatti è governata da una regola o formula ripetibile, così come la successione di Fibonacci.
In elettrotecnica [modifica]
Una rete di resistori, ad esempio un Ladder Network (Rete a scala), ha una resistenza equivalente ai morsetti A e B esprimibile sia come frazione continua che tramite la sezione aurea o ai numeri di Fibonacci difatti il rapporto Req/R = .